English 33-hole Board Example

Calculation by Moves

First a few definitions:

1. Let B_n be the set of board positions that can be reached from the starting position in n moves, but no fewer.
2. Let B_-n bet the set of board positions from which the finishing board position can be reached in n moves, but no fewer.
3. The complement board position is obtained by replacing every peg by a hole (i.e. removing it), and replacing every hole by a peg. For any board position b, the complement board position will be denoted b'. Similarly, for a set of board positions S, S' is the set of complement board positions. In other words b'∈S' if and only if b∈S.
4. |B_n| is the number of elements in the set B_n.

For the central game on the 33-hole English Board, the following table shows the size of the sets B_n and B_-n. The 8-fold symmetry of the problem was taken into account, but no resource count was used. Because of the symmetry of the problem, we really should refer to equivalence classes of board positions (this is important to realize when calculating set intersections). However, it simplifies our thinking if we select one representative board position from each equivalence class, so the sets B_n are sets of board positions.

n (level)	|Bn|	Ratio	Pegs	|B-n|	Ratio	Pegs
0	1		32	1		1
1	1	1.00	31	1	1.00	2
2	2	2.00	30	16	16.0	3-10
3	9	4.50	28-29	979	61.2	4-19
4	47	5.22	27-28	14,115	14.4	5-21
5	263	5.60	25-27	126,902	8.99	6-22
6	1,452	5.52	23-26	632,451	4.98	7-23
7	7,772	5.35	20-25	1,954,152	3.09	8-25
8	38,150	4.91	16-24	3,770,028	1.93	9-26
9	164,297	4.31	14-23	4,949,879	1.31	10-26
10	585,567	3.56	12-22	4,796,624	0.97	11-27
11	1,641,177	2.80	10-21	3,576,434	0.75	13-28
12	3,426,496	2.09	8-20	2,113,413	0.59	14-28
13	5,111,387	1.49	5-19	1,003,420	0.48	15-29
14	5,327,135	1.04	5-18	387,982	0.39	16-30
15	3,909,899	0.73	2-17	115,922	0.30	17-30
16	2,093,768	0.54	2-16	28,134	0.24	19-31
17	843,917	0.40	1-15	4,589	0.16	20-31
18	255,301	0.30	1-14	604	0.13	22-32
19	57,579	0.23	3-13	37	0.06	22-29
20	10,037	0.17	4-12	5	0.14	26-29
21	1,268	0.13	5-11	0	0.00
22	148	0.12	6-10
23	15	0.10	7-9
24	0	0.00
Total	23,475,688	~130 MB		23,475,688	~130 MB
Table 1: "Ratio" is |Bn|/|Bn-1|, or |B-n|/|B-(n-1)|. "Pegs" is the range in the number of pegs for all boards on this level. For a forward/backward search, only the green entries need to be calculated, only about 2% of the calculation time for this entire table (4-6 hours). See a similar table for the Wiegleb's Central Game

Note that the total number of boards in B_n or B_-n over all n are identical. This actually provides a good check that the algorithm is working properly, why must it be the case? If a specific board pattern b lies in some B_n, then by definition this board position is reachable from the central vacancy in n moves. Therefore it is possible to play from b' to the final state, but not necessarily in n moves, so b' must lie in some B_-m. In fact,
.

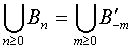Bergholt's 18 move solution can be recovered from B₁₈, B_-18, or the intersection of any B_n and B_-m where n+m=18. In an optimal search algorithm, one would clearly want to choose n to minimize the sum of the time to compute B_n plus the time to compute B_n-18. This occurs at about n=11, corresponding the green region of the above table, with total computation time on my machine about 8.5 minutes. This compares with over 2 hours for going all the way either forward or backward, so a significant time savings is realized by calculating both forward and backward.

The above table also contains some general results:

1. Any board position that can be reached from the central vacancy, can be reached in 23 moves or less.
2. Any board position that can be reduced to a single peg in the center can in 20 moves or less.

23 moves are required to reach these positions from the central vacancy. The positions with 9 pegs (the right three) can only be reached by using single jump moves. The rightmost board is also the only one (of 15 total) that can appear in a solution to the central game.
These positions can be reduced to a single peg at the center in a minimum of 20 moves. None of these board positions can appear in a solution to the central game. How do we know this? Because the complement cannot be reduced to a single peg.

One common peg solitaire puzzle is to take a given "shape" of pegs and attempt to reduce it to a single peg, usually in the center of the board. Once this "reduction problem" has been solved, we then can try to solve it in the smallest number of moves. If you try to solve the problem using a computer, checking each problem individually can take quite some time. Calculating the sets B_-m is a much more efficient way to proceed. Note that (by definition) every board pattern in B_-m can be reduced to one peg in m moves, and the set contains every possible pattern that can be so reduced. In a single (2 hour) calculation, we therefore have solved every conceivable reduction problem! The only constraint is that the jumps must all be made on the 33-hole board. Some of these problems can be solved in fewer moves if one allows jumps to holes that are not on this board, and there exist patterns of pegs on the 33-hole board that cannot be reduced to a single peg by using jumps on the board, but can be reduced to a single peg if jumps off this board are allowed.

Calculation by Jumps

1. Let S_n be the set of board positions that can be reached from the starting board position in exactly n jumps.
2. Let S_-n be the set of board positions from which the finishing board position can be reached in exactly n jumps.
3. Let W_n be the subset of S_n that can be reduced to the finishing board position (the "Winning positions").
4. Let N be the total number of jumps in a solution (31 for the single vacancy to single survivor problems on the English Board).

If the final board position is the complement of the initial board position, then in addition we have:

1. S_n = (S_-n)'
2. W_n = S_n ∩ (S_N-n)'.
3. W_n = (W_N-n)'.

n (level)	|Sn|	Ratio	Pegs	|Wn|	% Winning
0	1		32	1	100%
1	1	1.00	31	1	100%
2	2	2.0	30	2	100%
3	8	4.0	29	8	100%
4	39	4.88	28	38	97.4%
5	171	4.38	27	164	95.9%
6	719	4.20	26	635	88.3%
7	2,757	3.83	25	2,089	75.8%
8	9,751	3.54	24	6,174	63.3%
9	31,312	3.21	23	16,020	51.2%
10	89,927	2.87	22	35,749	39.8%
11	229,614	2.55	21	68,326	29.8%
12	517,854	2.26	20	112,788	21.8%
13	1,022,224	1.97	19	162,319	15.9%
14	1,753,737	1.72	18	204,992	11.7%
15	2,598,215	1.48	17	230,230	8.9%
16	3,312,423	1.27	16	230,230	8.9%
17	3,626,632	1.09	15	204,992	5.7%
18	3,413,313	0.94	14	162,319	4.8%
19	2,765,623	0.81	13	112,788	4.1%
20	1,930,324	0.70	12	68,326	3.5%
21	1,160,977	0.60	11	35,749	3.1%
22	600,372	0.52	10	16,020	2.7%
23	265,865	0.44	9	6,174	2.3%
24	100,565	0.38	8	2,089	2.1%
25	32,250	0.32	7	635	2.0%
26	8,688	0.27	6	164	1.9%
27	1,917	0.22	5	38	2.0%
28	348	0.18	4	8	2.3%
29	50	0.14	3	2	4.0%
30	7	0.14	2	1	14.3%
31	2	0.29	1	1	50.0%
Total	23,475,688	~130 MB		1,679,072	7.2%
Table 2: "Ratio" is |Sn|/|Sn-1|. "Pegs" is the number of pegs for all boards on this level. See a similar table for the Wiegleb's Central Game

Table 2 agrees with that calculated by "Durango Bill" [W9]. Note also that the total |S_n| over all n is the same as the total in the first table, calculated by move.

I have entered the (finite) sequences |S_n| and |W_n| into The On-Line Encyclopedia of Integer Sequences as A112737 and A112738.

If we take the union of W_n over n=0,2, ..., 15, we obtain a special set X of 839,536 board positions. What is so special about this set? If b(0) is any board position, let b(1), ... b(7) be the board positions obtained by all rotations and/or reflections of this board position, and b(8), ... b(15) be the complements of the first 8 board positions. Then b(0) can occur during a solution to the central game if and only if some b(i) is in X. This set X can be used to create a peg solitaire computer game with the ability to point out all winning moves from the current board position. If we use 33 bits to store each board position, then the set X requires around 4 MB of storage, hence can be easily held in memory.

Symmetric Board Positions

We can search S_n in Table 2 for symmetric board positions. This will give us all symmetric board positions which can be reached starting with the center vacant. Alternatively, we can take the complement of each board position—these are symmetric board positions where it is possible to finish with one peg in the center. This is the same as searching through th sets S_-n. We'll adopt the latter view in what follows.

There are seven possible types of symmetry for a configuration of pegs. The highest possible symmetry is square symmetry, in this case the board position is unchanged upon rotation by 90 degrees or reflection about the x or y axes (or either diagonal axis). There are 8 symmetry transformations which leave the board unchanged, forming the dihedral group D4. There are three order 4 subgroups of D4: 90 degree rotational symmetry, rectangular symmetry and symmetry about both diagonal axes, We also have three order 2 subgroups: 180 degree rotational symmetry, and reflection symmetry across one axis (orthogonal or diagonal axis). [In reality there are actually five order 2 subgroups, but the reflections form pairs. For example we have 34,500 board positions symmetric about the y-axis and another set of 34,500 which are 90 degree rotations of these, symmetric about the x-axis.]

If a board position has square symmetry, and it can be reduced to one peg, then this peg can only be at the center d4 or the equivalent holes from the rule of three: d1,a4,g4,d7. Why is this the case? It is because of the position classes. Suppose it is possible to finish somewhere other than the center. Then, because the board position is unchanged by 90 degree rotation, it must also be possible to finish at the same hole rotated through 90 degrees. But this will contradict the rule of three.

Similar reasoning shows that the same is true for the lower forms of symmetry, up until the last two. If we have only one reflection symmetry, we can finish on the axis of symmetry and not violate the rule of three.

Type 1: square symmetry 13 board positions	Type 2: 90 degree rotational symmetry 25 board positions	Type 3: symmetry across both diagonals 22 board positions	Type 4: rectangular symmetry 220 board positions
Type 5: 180 degree rotational symmetry 2,238 board positions	Type 6: Symmetry across y-axis (or x-axis) 34,500 board positions	Type 7: symmetry across one diagonal axis 5,139 board positions

The above table shows one sample board position of each type, followed by the total count of such board positions. Note that each board position is included in only the highest symmetry type (we do not count square symmetric positions in the lower symmetry types). You can now play the 279 positions of Type 1-4 on this Symmetric English Positions Javascript game. Try to solve each position to one peg in the center. Many of the larger patterns can be solved by reducing them to smaller symmetrical patterns. For more of a challenge, try solving each in the minimum number of moves.

In Beasley's book [B1, Chapter 10] he shows the 12 board positions with square symmetry which can be reached starting with the centre vacant (he does not count the starting position). Beasley also shows the 25 board positions with 90 degree rotational symmetry (he considers starting with the center vacant, so his board positions are all complements of our board positions). Table 3 shows a summary of these board positions by number of pegs and symmetry type.

n (level)	|Sn|	Pegs	Complement Pegs	Type 1	Type 2	Type 3	Type 4	Type 5	Type 6	Type 7
0	1	32	1	1	0	0	0	0	0	0
1	1	31	2	0	0	0	0	0	1	0
2	2	30	3	0	0	0	0	0	1	0
3	8	29	4	0	0	0	0	0	1	0
4	39	28	5	0	0	0	0	0	2	2
5	171	27	6	0	0	0	1	0	6	0
6	719	26	7	0	0	0	0	2	20	4
7	2757	25	8	0	0	0	1	3	43	6
8	9751	24	9	1	0	0	1	9	85	15
9	31312	23	10	0	0	0	1	9	170	21
10	89927	22	11	0	0	0	2	32	300	72
11	229614	21	12	1	0	1	0	26	548	56
12	517854	20	13	0	2	0	11	83	863	167
13	1022224	19	14	0	0	0	6	68	1365	204
14	1753737	18	15	0	0	0	13	166	1926	321
15	2598215	17	16	2	1	2	6	119	2622	363
16	3312423	16	17	0	4	4	22	274	3262	559
17	3626632	15	18	0	0	0	14	176	3808	540
18	3413313	14	19	0	0	0	25	347	4038	621
19	2765623	13	20	2	3	4	18	176	3876	566
20	1930324	12	21	0	8	5	23	275	3471	455
21	1160977	11	22	0	0	0	18	118	2742	443
22	600372	10	23	0	0	0	16	171	2114	269
23	265865	9	24	1	2	4	8	48	1414	220
24	100565	8	25	2	3	1	13	83	885	95
25	32250	7	26	0	0	0	4	20	501	87
26	8688	6	27	0	0	0	8	24	259	22
27	1917	5	28	1	1	1	1	5	117	24
28	348	4	29	1	1	0	5	3	45	5
29	50	3	30	0	0	0	1	0	13	2
30	7	2	31	0	0	0	2	1	2	0
31	2	1	32	1	0	0	0	0	0	0
Total	23475688			13	25	22	220	2238	34500	5139
Table 3: A count of boards with various symmetries. Type 1: square symmetry; Type 2: 90 degree rotational symmetry; Type 3: symmetry across both diagonals; Type 4: rectangular symmetry; Type 5: 180 degree rotational symmetry; Type 6: symmetry across x or y-axis; Type 7: symmetry across one diagonal axis See a similar table for the the French 37-hole board

Beasley [B1, Chapter 10] proves that a solution to the central game cannot pass through an intermediate board position with 90 degree symmetry. In order for this to be possible, there would need to be two positions among the 25 with 90 degree rotationl symmetry which are complements of one another. In [P9] Beasley proves that a solution to the central game cannot pass through an intermediate board position with 180 degree rotational symmetry.

We can now check each of the seven symmetry groups to see they contain a board position and its complement. We find that only the last two symmetry types can occur during solutions to the central game: symmetry across one axis (orthogonal or diagonal). We already know that the former is possible due to Martin Gardner's solution Jabberwocky. In Jabberwocky, the board passes through 9 intermediate states symmetric about the y-axis. With diagonal symmetry, the best I have been able to do is 7 intermediate symmetric board states.

Difficult Puzzles

Of course, if only a few jumps are possible from a certain board position, the winning jump is usually the obvious one. The most difficult board positions would seem to be those having as many jumps as possible, but only one winning jump. For each n (or number of pegs p=32-n), we can identify such board positions. Sometimes there is even a unique board with p pegs with exactly one winning jump and as many total jumps as possible.

6 pegs; 7 jumps Play this puzzle now	12 pegs; 13 jumps Play this puzzle now	17 pegs; 17 jumps† Play this puzzle now	23 pegs; 11 jumps Play this puzzle now
Positions with as many jumps as possible but only one winning jump. † means the board position is unique (this is the only board position with 17 pegs, 17 possible jumps, and one winning jump).

Above we see four positions found by this technique, with 6, 12, 17 and 23 pegs. All are solvable to one peg in the center, but only one starting jump leads to a solution. For the first puzzle, the board shape is unimportant, we might as well present this problem on an infinite board. Some of the larger puzzles may no longer have a unique winning jump when played on an infinite board. The 23-peg position, for example, has additional winning jumps when played on an infinite board.

Aside from the first one, these puzzles tend to be challenging to solve by hand. However, knowledge that there is a unique winning jump can help solve the puzzle. For example, after this first jump is executed, all jumps which could have been performed as a first jump must still be dead ends. The second jump can only be some jump opened up by the first jump, and so on. If you can identify the winning first jump, sometimes the rest of the solution follows more easily. Note that since these board positions have no symmetry, we could also consider finishing locations other than the center. Each finishing location produces a whole new set of puzzles, although many of them may be the same or similar to others.

You can now play all 45 puzzles with 4 to 27 pegs (finishing in the center) on my Difficult English Positions Javascript game.

Can the puzzle be solved by jumping randomly?

The symmetry of the board must be carefully considered in this calculation. As before we consider board positions that are identical via reflection and/or rotation as the same board position. For example after the first jump there are four possible board positions, however since these are all rotations of each other we consider this as only one board position, which occurs with probability 1. Things become more complicated later in the game, because two completely different jump sequences may result in board positions that are exact 90-degree rotations of each other (for example), which by our accounting are the same board position.

Looking at the last column of Table 2, you may conclude that if our random player makes 15 jumps, there is an 8.9% chance that the board is still in a "winning position" (can be reduced to one peg assuming perfect play). However, this type of reasoning is incorrect because it assumes each board position is equally likely, which is actually far from true. In fact a random player is much less likely to remain in a winning board position, and after 15 random jumps the chance that the board is in a winning position is less than 1%.

Table 4 below shows where a randomly played game is likely to end. A "dead end" is a board position from which no jump is possible (game over), and we show the number of dead ends, and the probability that the game ends after exactly n jumps. The probability that the central vacancy start finishes with one peg (at either the center d4, or d2, b4, f4 or d6) is 2.6978E-08, or about 1 in 37 million games. The probability that the final peg ends up in the center is exactly half this, or 1 chance in 74 million (even on the final jump, our random player has a 50% chance of going the wrong direction).

n (jump)	Pegs left	Dead ends	Probability that the game ends after n jumps
6	26	1	7.4074E-03	exactly 1 in 135
7	25	0	0	never
8	24	0	0	never
9	23	0	0	never
10	22	1	9.7435E-06	1 in 102,633
11	21	1	6.8999E-05	1 in 14,493
12	20	0	0	never
13	19	5	5.7230E-05	1 in 17,473
14	18	10	1.0757E-04	1 in 9,296
15	17	7	2.6607E-04	1 in 3,758
16	16	27	1.7353E-04	1 in 5,763
17	15	47	6.6371E-04	1 in 1,507
18	14	121	1.4401E-03	1 in 694
19	13	373	4.1355E-03	1 in 242
20	12	925	9.8602E-03	1 in 101
21	11	1972	2.5485E-02	1 in 39
22	10	3346	7.6543E-02	1 in 13
23	9	4356	1.5044E-01	1 in 6.6
24	8	4256	1.9958E-01	1 in 5.0
25	7	3054	2.4665E-01	1 in 4.1
26	6	1715	1.6347E-01	1 in 6.1
27	5	665	7.9883E-02	1 in 13
28	4	182	3.0672E-02	1 in 33
29	3	39	3.0107E-03	1 in 332
30	2	6	7.7690E-05	1 in 12,872
31	1	2	2.6978E-08	1 in 37.07 million
Total		21,111	1.0000E+00
Table 4: How the game will end if a player selects jumps at random. Calculated exact values from level calculations, probabilities confirmed by Monte Carlo simulation.

Our random player is expected to finish most often with 7 pegs, and with a mean of 7.64 pegs. If we compare these results with those of "average" human players, we find that most are able to do quite a bit better than this. The reason, of course, is that human players do not select jumps at random. Most people will try to clear out the arms without stranding a peg near the edge of the board, and a lot of people can get down to 2 or 3 pegs after 10 attempts or less.

While a modern computer can simulate a million games in a matter of seconds, such a brute force technique expends an awful lot of effort to find a single solution, and will fail entirely for larger boards. Making random jumps is actually one of the worst strategies to adopt in solving the central game.

Finally, it is interesting to find the most and least likely ending board positions for a randomly played game:

The most likely finish to a random game, also the shortest possible game (6 jumps). One out of every 135 randomly played games ends at this board position. What six jumps are needed to reach this board position?	The least likely finish to a random game. One out of every 70.4 billion randomly played games ends at this board position. Can you figure out how to reach this board position? Hint: Where must the pegs at d2, b4, d4 and f4 have started from?

Finding and Counting Minimal Length Solutions

The Solution Graph

The nodes of the solution graph are the board positions along minimal length solutions, and the links joining them are the moves between these board positions. As a result of our calculation by levels, we already have some of these board positions, namely those in the intersection between the forward and backward level sets (B₁₁ and B_-7 in our example). To recover all the board positions in any minimal length solution, it is just a matter of tracing these board positions both backward and forward in the level sets.

The solution graph for the English central game is shown below. The left node (B) is the board position with the central vacancy, while the right node (E1) is the final board position with one peg in the center. This graph was produced by Sidney Cadot. He uses a different notation for moves and board locations (he numbers the holes consecutively 1-33).
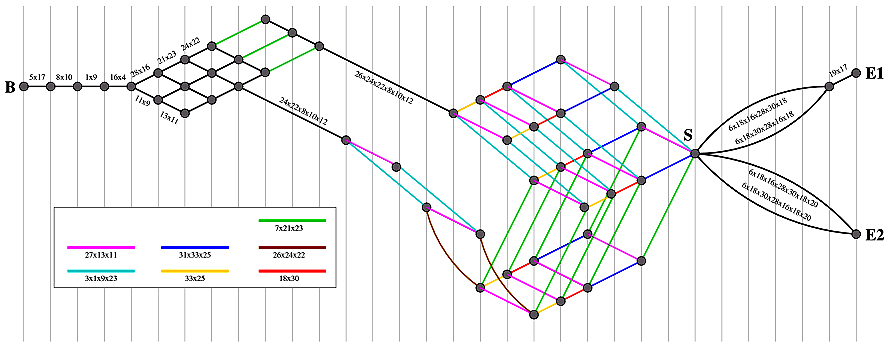
Note that Sidney has arranged the graph horizontally so that positions with the same number of pegs lie on a vertical line. I would align boards vertically by level, which would show that they all contain the same number of moves. The figure below shows one of the possible 18-move solutions to the central game (first found by Ernest Bergholt in 1912).

Two Ways to Count Solutions

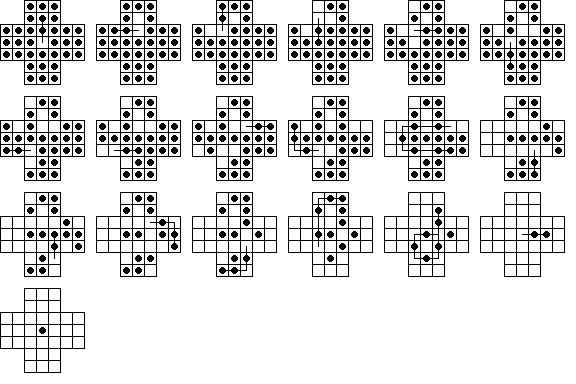
936 sounds like quite a few solutions, but most of these solutions have the exact same moves, just in a different order. Can we quantify this? If you look at the solution graph, you can see that there are really only two different paths to take. If you don't count the order of moves, there are really only two solutions. The top route in the solution graph is taken by the above solution, while the lower route is that taken in the solution below. As you can see, the difference between these solutions is quite subtle.

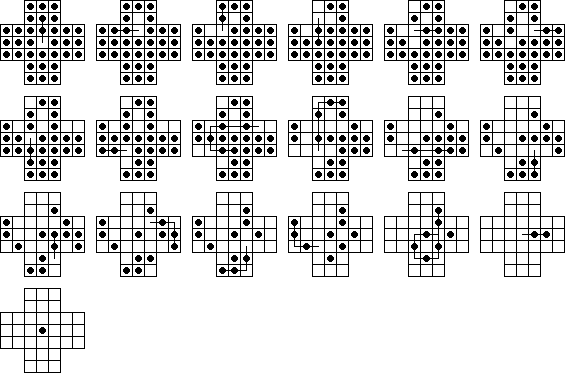
To count solutions regardless of move order, a similar, although somewhat more complex algorithm is used. At each node, instead of having a single number to keep track of, I use a sequence of lists, each of which is a set of moves that can used to reach that node, not counting order. These lists are sorted (in some known, but arbitrary order) so we can easily check for duplicates. Going through the tree in the same fashion, the number of solutions regardless of move order is the number of lists at the terminal node, and each list gives a possible solution.

Also, when all is done you have lists of solution moves, but you no longer know how to order the moves to make them solutions! Figuring out an order that will make it work can be non-trivial, so I found that at each node in the tree I wanted to store BOTH a sorted move list and the original (sequential) move list. This way at the end one can go back to the original list and recover each solution.

By the way it is also possible to use the same technique for solutions calculated by jump. In other words, we consider solutions of any length and consider them as sequences of jumps (not moves). The number of solutions to the central game regardless of jump order is extremely large and the memory on my PC fills up before this calculation is complete. However, I have been able to complete this calculation on smaller boards, particularly the triangular peg solitaire boards. In this case, the counting is a bit strange, for example a solution to a complement problem and the jumps executed in the exact reverse order are considered the same solution. This oddity doesn't happen when counting minimal solutions, because when such a solution is reversed it is almost never minimal length. But some counter-intuitive behavior can still occur, as shown in the next section.

An Additional Subtlety and Solution Classification

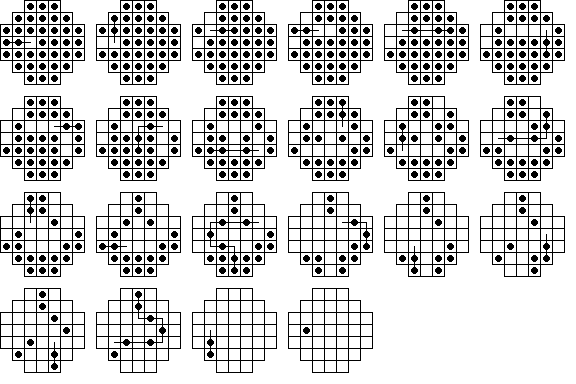
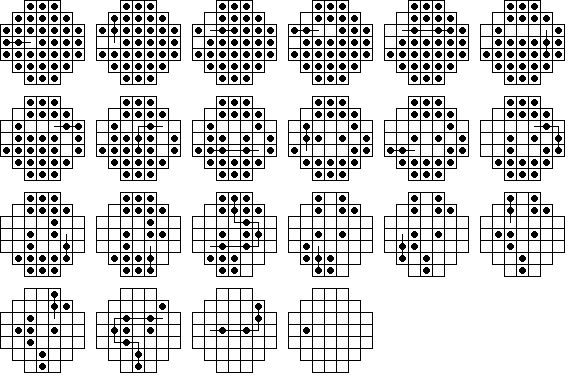
These two solutions have the first nine moves identical, but after that they appear to be different, and they finish very differently. However a careful check will show they actually contain exactly the same moves, just in a different order. Thus, according to our accounting method, they are the same solution, even though their endings are completely different. Therefore, when grouping solutions regardless of move order, there is no longer a unique finishing move. The situation above is a rather unusual occurrence and is not true for the vast majority of cases (usually solutions with the same moves differ only in the middle), but must be taken into account for the general case. Although there is no unique final move, there is a definite longest final sweep length for any solution no matter what order it's moves are taken in (3 in the above example). Therefore, I now classify solutions according to three numbers (A,B,C):

1. Length of the longest sweep
2. Length of the second longest sweep
3. Length of the (longest possible) final sweep

Created in 2007. Last modified May 20th, 2016

Copyright © 2014 by George I. Bell

Peg Solitaire Main Page ...